#include <bits/stdc++.h>
using namespace std;

class Sunnygraphs {
public:
 map<int,bool> mp;
 void func(int &cnt,int p,vector<int> &a){
 while(!mp[p])mp[p]=true,cnt++,p=a[p];
 }
 
 long long count(vector <int> a) {
 int n=a.size();
 int ac=0,bc=0,cc=0,dc=0;
 mp.clear();
 func(ac,0,a);
 func(bc,1,a);
 mp.clear();
 func(cc,1,a);
 func(dc,0,a);
 int C=n-ac-bc;
 long long ans=(1LL<<n);
 ans-=((1LL<<bc)-1LL)*(1LL<<C);
 ans-=((1LL<<dc)-1LL)*(1LL<<C);
 if(ac==dc)ans-=(1LL<<C);
 return ans;
 }
};

変数acは、エッジを向有としたとき（ i 番目のノードから a[ i ] 番目のノードに向かってエッジを張る）に、0のノードから到達可能なノードの個数です。

変数bcは、0のノードからは到達可能だけれど、0のノードからの到達が不可能なノードの個数です。

似たような感じで、ccは1から到達可能、dcは0から到達で1から到達不可能なノードの個数です。

acとdcが等しいときは、0のノードと1のノードが異なる連結成分に存在していることになります。

2016-04-27

【No.018】「 AOJ-ICPC 550 引っ越し」

House Moving | Aizu Online Judge

この問題を解くためには、

元の数列の総和から、「その数列から任意の長さの部分増加列を取り出して、その増加部分列の要素の総和を最大化したときの値」を引けばよいです。

サンプル1ならば、

元の数列 : { 1, 4, 2, 3 }

元の数列の総和 = 1+4+2+3 = 10

総和が最大の増加部分列 : { 1, 2, 3 }

増加部分列の総和 = 1+2+3 = 6

よって、10-6=4が答えになります。

※要するに増加部分列に採用されなかった項は、体力を消費して動かすことになる。

サンプル4ならば、

元の数列 : { 6, 2, 1, 3, 8, 5, 4, 7 }

元の数列の総和 = 6+2+1+3+8+5+4+7 = 36

総和が最大の増加部分列 : { 2 , 3 , 5 , 7 }

増加部分列の総和 = 2 + 3 + 5 + 7 = 17

答え = 36 - 17 = 19

総和が最大になる増加部分列を求める問題をO( n^2 )で解く場合、どの項に着目しているかを状態に持って、次にどこの項を採用するかで遷移するDPになります。

このとき、遷移にO(N)かかってしまうところを、セグメントツリーやBITをつかうことでO( log N ) で遷移できるようになります。

2016-04-26

【No.017】「AOJ-ICPC 500 それぞれの感想前編」

f:id:dohatsutsu:20160426200644p:plain

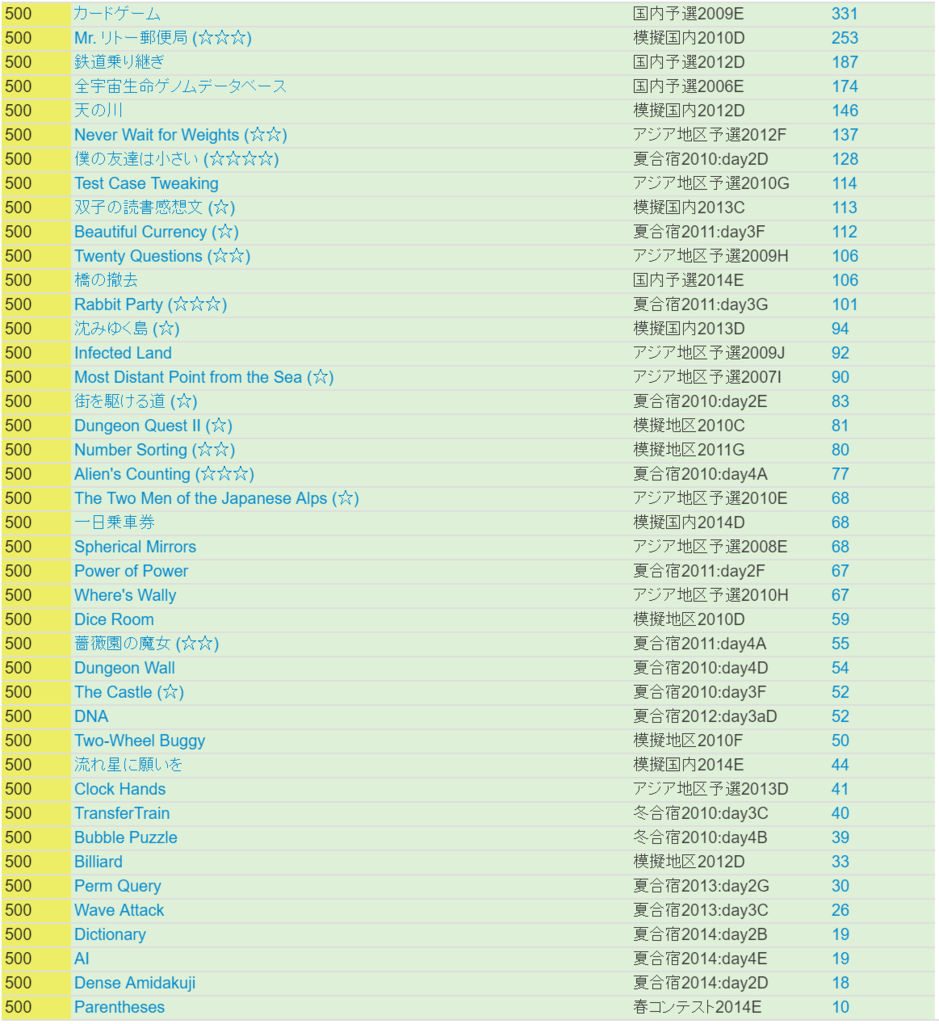
aoj-icpc 500 が埋め終わりました。 pic.twitter.com/kEVJ2cXTuT
— 怒髪 (@dohatsutsu) April 26, 2016

今回は、AOJ-ICPC 500 にある問題（42問）について、感想をひとつずつ書いていこうと思っています。

○カードゲーム

Cards | Aizu Online Judge

AIZU ONLINE JUDGE: Code Review

学部2年の5月、蟻本のp197にある二部マッチングのコードの使い方を練習するために解いた記憶があります。

68行目に V=m; とあるけれど、これはどうなんだろう・・・・。

このエッジの張り方だと、別に問題はない。（そもそも実際にACしている）

だけど、ノードの数を表す変数としてVを用意しているのなら V=n+m が正しいと思う。

（このときはまだ中身をよく理解していなかったからしかたない）

○Mr. リトー郵便局

Mr. Rito Post Office | Aizu Online Judge

AIZU ONLINE JUDGE: Code Review

学部2年の6月に解いた問題。

なぜかすごく印象に残っていて、今でも概要と解法を覚えているくらい。

それだけ解けたときに嬉しかったんだと思う。

○鉄道乗り継ぎ

Railway Connection | Aizu Online Judge

AIZU ONLINE JUDGE: Code Review

学部3年の6月末(チームFinalZukkyとして国内予選に参加する数日前)に解いたっぽい。

この問題を解いたことによって得られた経験がその国内予選での結果につながったかどうかはかなり怪しい。

○全宇宙生命ゲノムデータベース

The Genome Database of All Space Life | Aizu Online Judge

http://judge.u-aizu.ac.jp/onlinejudge/review.jsp?rid=1181781#1

学部2年の1月に解いた問題。

再帰関数で素直に最初の文字から1文字ずつ求めていって、i 文字目が分かったら即、再帰関数を終了するようにしました。もっと賢いやり方があるかもしれないけど、この方法はあまり面倒ではないのでこの方法で求めました。

○天の川

Milky Way | Aizu Online Judge

AIZU ONLINE JUDGE: Code Review

学部3年の7月に解いた問題。

線分どうしの距離を求める方法を自力で思いつける人はどのくらいいるのだろうか・・・。（僕は本で知りました。）

○Never Wait for Weights

Never Wait for Weights | Aizu Online Judge

AIZU ONLINE JUDGE: Code Review

部活の練習中にUnionFindを使うというネタバレを受けてしまったため、

完全に自力で挑戦して解いた問題ではないです。

結構バグを取るのに時間がかかった思い出があります。

○僕の友達は小さい

My friends are small | Aizu Online Judge

AIZU ONLINE JUDGE: Code Review

学部3年の7月に解いた問題で、結構面白かった。

最初は全く解法が思いつかず、翌日になってもう一度考察してみたらあっさりと解けた思い出があります。

問題文に「なお1,000,000,007 は素数である。」と書いてあるのを初めて見ました。

○Test Case Tweaking

Test Case Tweaking | Aizu Online Judge

AIZU ONLINE JUDGE: Code Review

個人的に解法を考えるのに時間がかかってとても悔しかった問題です・・・。

○Beautiful Currency

Beautiful Currency | Aizu Online Judge

AIZU ONLINE JUDGE: Code Review

個人的に計算量がよく分かっていないです。

n/1+n/2+n/3+...+(n-1)/n+n/n って意外と小さいっぽい？

2016-03-21

【No.016】「今更すぎるパソコン甲子園2012参加記?」

高校3年の4月、高校の数学の先生から「かなり勉強しないと会津大学の合格は難しい」と言われた。（このときまで僕は数学ABという科目の存在を知らなかった）

毎日、部活が終わった後はすぐに家に帰って数学ABの勉強をするようにした。（約3カ月続けた）具体的には教科書を読みながら例題と章末問題を解いていった。分からないところがあったときは次の日に高校の先生に聞きに行った。

パソコン甲子園の練習もしたかったけれど数学の勉強で忙しかったし家にネット環境も無いからできなかった。

夏休みに入る頃には数学ABの勉強が一通り終わったので数学IIの勉強をはじめた。

そして9月上旬、パソコン甲子園の予選があった。

All Numbers Lead to 6174 | Aizu Online Judge

まず始めに僕が30分かけてこの問題を解いた。

Points for a Perfect Scorer | Aizu Online Judge

Railway Ticket | Aizu Online Judge

この2つは僕が別の問題の解法を考えている間にチームメイトに解いてもらった。

Kitchen Garden | Aizu Online Judge

何分かかったかは覚えていないけれど、うまく場合分けをしてO(n)で解いた思い出がある。

初めから等差数列になってるような入力は存在しないと勝手に思っていた。

結果は4問ACで22位。地域枠として本選に行くことができた。

ちなみにこの年は10回目記念で本選に進出したチーム数が32チームとなっていた。

11月の上旬、本選に参加するも1問しか解けなかった。

Aka-beko and 40 Thieves | Aizu Online Judge

この問題を解くのに2時間もかかってしまった。

（javaのString型で i 文字目にアクセスする方法を知らなかったため）

持ち込んでいた資料の中からいろいろ探した結果、 split を使ってACした。

残りの2時間はチームメイトに

Triangle of Blocks | Aizu Online Judge

を任せつつ、残りの問題を考察していた。

12月の上旬、会津大学の合格発表があった。

12月の末から4月になるまでの間は数学C、数学III　の勉強をした。

2016-03-20

【No.015】「JOIOIの塔貪欲法」

Tower of JOIOI | Aizu Online Judge

この問題を解いた後、JOIのページに行くと想定解が二分探索で、O(N long N)でした。

僕の解法は貪欲法でO(N)でした。

今回はその簡単な解説を行いたいと思います。

つくりたいものがJOIのみだった場合、以下のようなコードになるはずです。

#include<bits/stdc++.h>

using namespace std;

int n,J,JO,JOI;

char str[1000001];

int main(){

  scanf("%d",&n);

  scanf("%s",str);  

  for(int i=0;i<n;i++){

    if(str[i]=='J'){

      J++; // Jをつくる

    }else if(str[i]=='O'){

      if(J>0){ // Jが作られていたら、それを1つ使ってJOを作る。

        J--; // 残っていなかったらこのOは決して使われない。

        JO++;

}

    }else if(str[i]=='I'){

      if(JO>0){ // JOが作られていたら、それを1つ使ってJOIを作る。

        JO--; // 残っていなかったら、このIは決して使われない。

        JOI++;

}

}

}

  cout<<JOI<<endl;

  return 0;

}

しかし、今回はIOIでもよいため、工夫が必要になります。

'J'を読んだときは'I'を作るようにします。

'O'を読んだときは、'I'が余っていれば'IO'を作ります。'I'が余っていないときは、すでに完成している 'IOI' を分解して 'IO'　を2つ作るようにします。

Iを読んだときは、'IO'が余っていたらそれを使って'IOI'を作るようにします。

※ただし、分解によって作られたIOはなるべく使わず、普通に作られた'IO'を優先的に使うようにする。

余っていなかった場合は'I'を作るようにします。

（分解することによって作ったのにも関わらず余ってしまった'IO'をくっつけて元に戻すようすることを最後に行います)

#include<bits/stdc++.h>

using namespace std;

int n,I,IO,IOI,cnt;

char str[1000001];

int main(){

  scanf("%d",&n);

  scanf("%s",str);  

  for(int i=0;i<n;i++){

    if(str[i]=='J'){

      I++; // Iを作る

    }else if(str[i]=='O'){

      if(I>0){

        I--; // Iを1つ使ってIOを作る

        IO++;

      }else if(IOI>0){

        IOI--; // Iが残っていないときはIOIを分解してIOを2つ作る

        IO+=2;

        cnt+=2; // この方法によって作られたIOの数を数えておく

}

    }else if(str[i]=='I'){

      if(IO>0){

        IO--; //IOを使ってIOIを作る。

        if(IO<cnt)cnt--;//使用したIOが分解によって作られたものかどうかを判定

        IOI++;

      }else{

        I++;　// Iを作る

}

}

}

  cout<<IOI+cnt/2<<endl;　// +cnt/2 は分解しすぎたIOIをもとに戻す処理

  return 0;

}

2016-03-20

【No.014】「僕が高校生のとき」

僕が競技プログラミングに出会ったのは今からちょうど4年前で、2012年の3月の末でした。（僕が高校3年生になる約一週間前）

それまでの僕のプログラミング歴は、地元の商業高校の授業で2年間COBOLを使い二分探索やバブルソートを実装したことがあるだけで、プログラミングがどちらかというと嫌いでした。（家にインターネットはなかった）

また、家が貧しいので高校を卒業した後は就職するつもりでいました。（就職先はまだ考えていなかったけど）

ーーーーーーーーーーーーーー

そもそものきっかけは、会津大学の公開講座への参加を高校の先生に誘われたことでした。

そのとき僕はとくに断る理由もなかったのでとりあえず参加することにしました。

その講座ではもちろんCOBOLなんかは使えないため、参加する数日前に先生からjavaの書き方を教えてもらいました。

そして公開講座当日、僕は競技プログラミングの存在を知り、簡単なパソコン甲子園の過去問を解いたりしました。（二分探索をやるだけの問題とか）

その講座で僕は完全に競技プログラミングにのめり込みました。

2週間後、高校3年4月の三者面談で、僕は進路を就職から会津大学への進学に変更することになりました。

つづく

dohatsutsu’s diary

日記を書いています。

【No.020】「ICPC 2016 国内予選 E問題 3Dプリント」

【No.019】「 SRM 691 div1 easy 」

【No.018】「 AOJ-ICPC 550 引っ越し」

【No.017】「AOJ-ICPC 500 それぞれの感想前編」

【No.016】「今更すぎるパソコン甲子園2012参加記?」

【No.015】「JOIOIの塔貪欲法」

【No.014】「僕が高校生のとき」